The Kinetic Monte Carlo (KMC) method simulates the statistical process of ion migration in a defined lattice by weighting kinetic probabilities through the generation of random numbers. The probability that a jump attempt is successful depends on the migration energy Emig and is given by
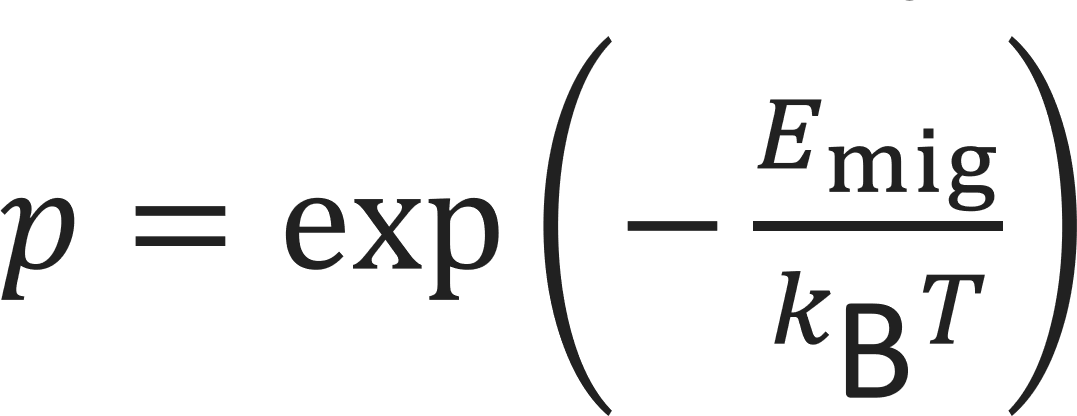
The KMC algorithm follows the following process:
The ionic conductivity is given by the concentration c, charge q and the electrical mobility μ of the mobile ions:
From the Kinetic Monte Carlo simulations, the mobility can be directly obtained by applying an electric field 
. Then, the conductivity is given by the displacement of the mobile ions in the electric field and the simulated time:
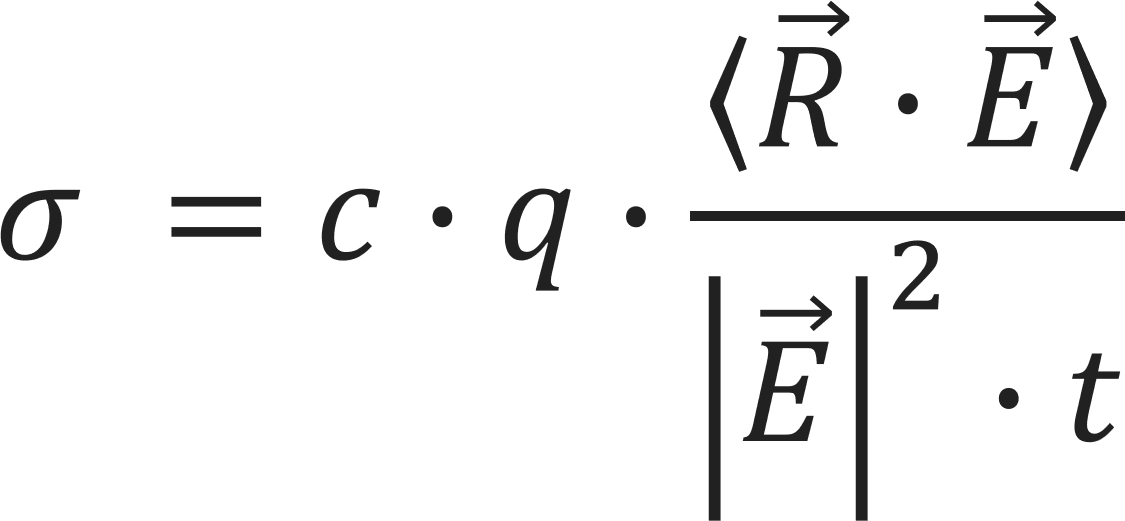
The time is calculated from the number of jump attempts Natt, the number of mobile ions Nc, the number of possible jump directions Np and the attempt frequency ν0 that determines the number of jump attempts per time.
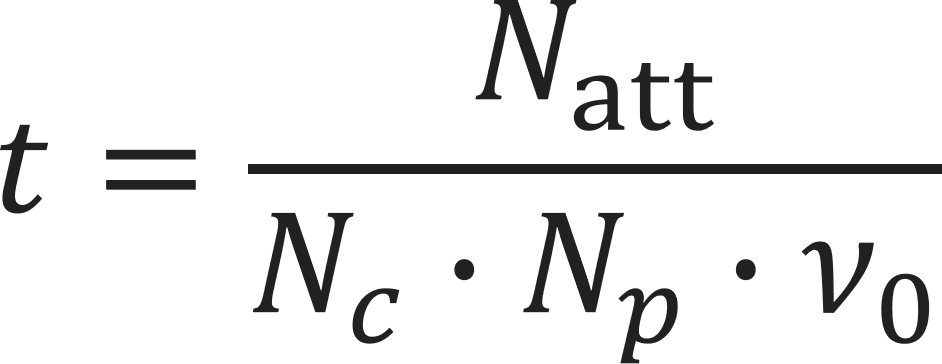
The applied electric field is typically stronger than under experimental conditions. For strong electric fields, the mean displacement of the ions in the field is large and the migration statistics improve. However, the field has to be weak enough such that its influence is small compared to the migration energies.
For more information, see the introduction paper of iCon:
P. Hein, B.O.H. Grope, J. Koettgen, S. Grieshammer, M. Martin, iCon: A general lattice Kinetic Monte Carlo program, submitted.